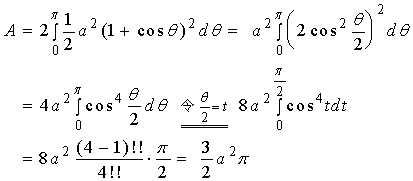§6.2
平面图形的面积
一、直角坐标的情形
由曲线![]() 及直线
及直线 ![]() 与
与 ![]() (
( ![]() ) 与
) 与 ![]() 轴所围成的曲边梯形面积
轴所围成的曲边梯形面积![]() 。
。
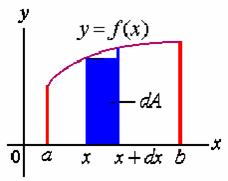
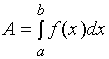 其中:
其中:![]() 为面积元素。
为面积元素。
由曲线 ![]() 与
与 ![]() 及直线
及直线 ![]() ,
,![]() (
( ![]() )且
)且![]() 所围成的图形面积
所围成的图形面积![]() 。
。
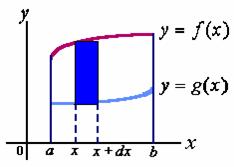
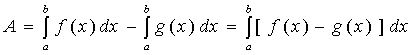
其中:![]() 为面积元素。
为面积元素。
【例1】计算抛物线![]() 与直线
与直线![]() 所围成的图形面积。
所围成的图形面积。
解:1、先画所围的图形简图
解方程
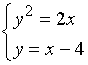 , 得交点:
, 得交点:![]() 和
和 ![]() 。
。
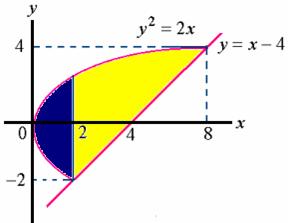
2、选择积分变量并定区间
选取![]() 为积分变量,则
为积分变量,则![]()
3、给出面积元素
在![]() 上,
上, 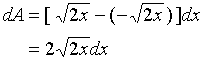
在![]() 上,
上, 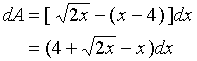
4、列定积分表达式
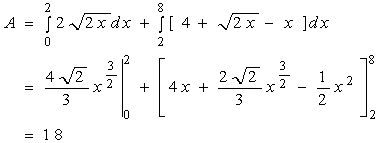
另解:若选取![]() 为积分变量,则
为积分变量,则 ![]()
![]()
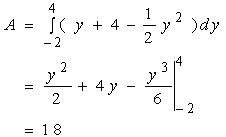
显然,解法二较简洁,这表明积分变量的选取有个合理性的问题。
【例2】求椭圆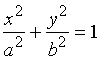 所围成的面积
所围成的面积 ![]() 。
。
解:据椭圆图形的对称性,整个椭圆面积应为位于第一象限内面积的4倍。

取![]() 为积分变量,则
为积分变量,则 ![]() ,
, 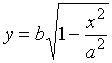
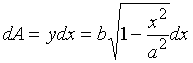
故 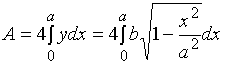 ( * )
( * )
作变量替换 ![]()
![]()
则
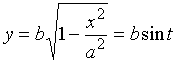 ,
, ![]()
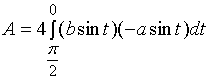 ( * * )
( * * )


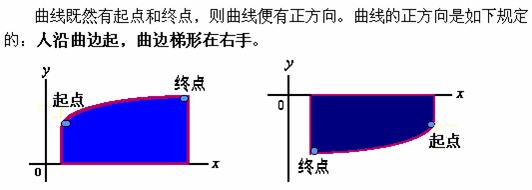
于是,我们可给出曲边梯形的曲边由参数方程给出时,其面积计算公式
设曲边梯形的曲边由参数方程
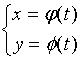
给出,曲边梯形的面积计算公式为
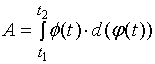
其中:![]() 及
及![]() 分别曲线的起点与终点的所对应的参数值。
分别曲线的起点与终点的所对应的参数值。
二 极坐标情形
设平面图形是由曲线
![]() 及射线
及射线![]() ,
,![]() 所围成的曲边扇形。
所围成的曲边扇形。
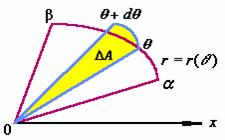
取极角![]() 为积分变量,则
为积分变量,则 ![]() ,在平面图形中任意截取一典型的面积元素
,在平面图形中任意截取一典型的面积元素![]() ,它是极角变化区间为
,它是极角变化区间为![]() 的窄曲边扇形。
的窄曲边扇形。
![]() 的面积可近似地用半径为
的面积可近似地用半径为![]() , 中心角为
, 中心角为![]() 的窄圆边扇形的面积来代替,即
的窄圆边扇形的面积来代替,即
![]()
从而得到了曲边梯形的面积元素
![]()
从而 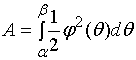
【例3】计算心脏线![]() 所围成的图形面积。
所围成的图形面积。
解:
由于心脏线关于极轴对称,